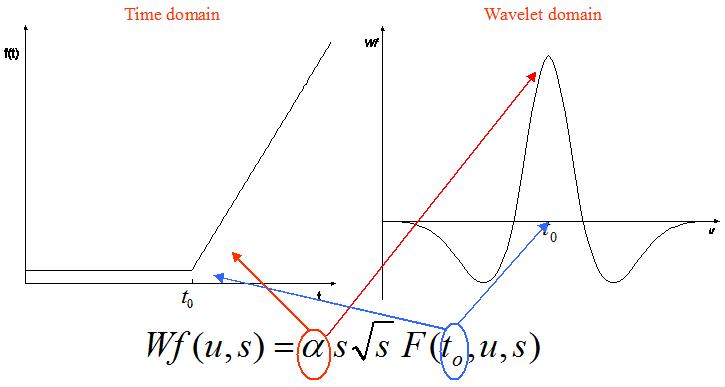
Idea: instead of trying to follow the wavelet coefficients of a generic signal along scales, a simple signal with just one singularity is considered (see the picture below-left). In the wavelet domain, it corresponds to a shape like the one shown below-right, whose location t0 is the same, while its amplitude is tied to the slope α of the straight line in the time domain. The shape has been achieved using a 3/9 spline biorthogonal wavelet basis. Its equation in the wavelet domain can be proved to be the one written in the picture (for more details see [1]).
For 'more complicated' singularities, the atomic approximation still considers the same shape (and the relative equation) above, i.e. the one generated by two straight lines. An example is shown below where the blue shape is the one generated by the signal on the left while the red one is the approximating atom:

This approximation may seem too coarse. However, it allows to overcome some limits of other approaches, since it allows us to manage more complicated signals (like a row of Lena, for instance). In fact, in practical cases we have many singularities (and then many atoms). Thanks to the use of just one atom and its symmetric shape, we can exploit the linearity of the wavelet transform or the overlapping effects principle . In this way, any limit about the maximum scale level of the wavelet expansion is required. A simple example of two simple signals (each one containing two singularities) and their wavelet coefficients at different scale levels is shown below.

From the picture above, it can be seen that that it may happen:
- the atoms have the same sign, both positive or negative (as in the example above.left). If they are closer than the cone of influence at that scale, there is an attractive effect. They interfere more and more till they become an only atom with an energy equal to the sum of their energy and a shape equal to that of the atom. The location of the new atom is the center of mass, i.e. the motion of each atom is inversely proportional to its energy (or mass).
- the atoms have opposite signs, positive-negative or negative-positive (as in the example above.right). If they are closer than the cone of influence at that scale, there is a repulsive effect. They interfere more and more till they become an only atom with an energy equal to the sum of their energy and a shape equal to that produced by a step singularity in the wavelet domain (see the example above). The location of the new atom is in the center of mass, i.e. the motion of each atom is again inversely proportional to their energy (or mass).
If the atoms are characterized by their greatest estremum (maximum or minimum), the two kinds of interference can be discriminated by tracing atoms trajectories:

Note: trajectories have no interruptions even though we do not use a wavelet that is derivative of a gaussian kernel. This is possible since the proposed theory refines the existing ones, as it will be clearer in the following --- please compare them with the ones traced in other existing approaches (Mallat, Perona-Malik etc...). Obviously, this also holds for signals with more (than two) singularities as well as for real signals (a row of Lena, for instance).
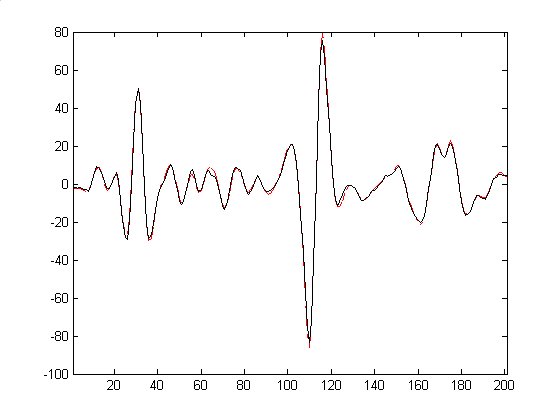
But, probably a video is more clear than many words...
Below there are three sequences: the first one is relative to one isolated atom! The other two are relative to the two possible cases of interference.
Two atoms with the same sign (attraction)
Two atoms with opposite sign (repulsion)
Note: When two atoms completely interfere, it is not possible to go back: the new 'generated' singularity cannot (in principle) be split in the two ones that originated it, in absence of additional information. Thus, the process depicted above, that has been formalized below, is not reversible! In the applications we will see that 'we will have to pay' the additional information (at any junction from the coarser to the finer scales) about the origin of the considered atom (if or not it has been produced by two or more atoms).
Is it possible to formally write all this? The answer is yes!
It can be formally proved that the interference, or more precisely, the evolution of the atoms along scales can be described by pdes[3]. In particular, the pde which describes the time scale behavior of one atom is the following:

where s indicates the scale, u the time, t0 the singularity location, ω the wavelet transform while ωu and ωs the partial derivatives of the wavelet transform with respect to u and s.
This equation contains a diffusive (atom domain grows for increasing scales) and source (atom amplitude also grows) effect.
It can also be derived the trajectory in the (u,s) plane of the (absolute) maximum of the atom:
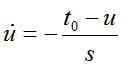
It is a straight line: the atom doesn't move form its initial location.
This result can be generalized to the case involving many atoms whose equation becomes:
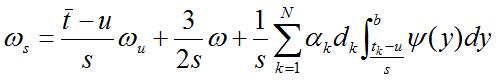
The last term accounts for the attractive (or repulsive) effect, while the time-scale trajectories are now described by the following ordinary differential equation:
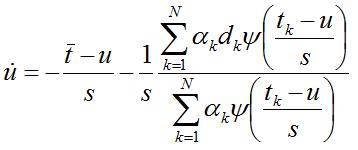
Obviously, the trajectories are no more straight lines but depend on the slopes of the atoms and their distances (see the last term of the pde for more atoms).
But, so far we have not considered that the approximation of any singularity by (coarsely speaking) a first order one has an uncorrect decay along scales [4]. Then, we have to compensate it with the right Lipschitz coefficient ϒ . We can then define the generalized atom as follows:
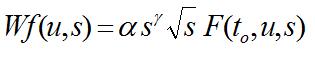
whose law becomes:

that generates the following time-scale trajectories for many (generalized) atoms:
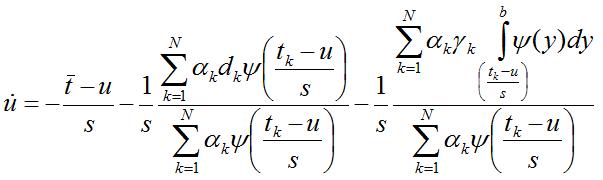
Summing up
From a wavelet detail band (usually the one at the first scale level) atoms are 'extracted' via a very fast matching pursuit algorithm (just one atom shape is considered). In practice, estrema (maxima and minima) are computed and ordered in a decreasing order. Starting from the highest one, the location t0 corresponds to the extrema one. The atom amplitude α is estimated by least squares [1]. It is then subtracted from the wavelet band and all the process is repeated till all atoms have been considered. This phase gives us the number of atoms and their amplitude and position. In order to estimate the Lipschitz coefficients ϒ , the ordinary differential equation above has to be numerically solved for a few scale levels (they have to be very close for giving a correct result) [2]. It can be used the fourth order Runge-Kutta scheme. Once we have all the three required parameters for each atom
we are able to predict the position of any atom at any sucessive scale level, as well as its speed for reaching the new position (due to repulsion and/or attraction with the closest atoms)!
You may ask now whether all this can be useful in practice. The answer is, again, positive.
Obviously, the results above have to be adapted to the specific application at hand. For instance, one cannot think of numerically solving the ordinary differential equation above for a problem of coding or a more robust scheme may be required in case of noise. However, some tricks can be exploited for overcoming these limits.
Below, there are some applications with comparisons with alternative approaches in literature that show the great potentialities of this theory:
References:
- V. Bruni, D. Vitulano (2006). Wavelet based Signal De-noising via Simple Singularities Approximation. Signal Processing Journal, Elsevier Science, Vol. 86, pp. 859-876, April 2006.
- V. Bruni, B. Piccoli, D. Vitulano (2008). Wavelets and pde for image de- noising. Electronic Letters on Computer Vision and Image Analysis (ELCVIA), Special Issue on Partial Differential Equations Methods in Graphics and Vision, vol. 6, no. 2, pp. 36-53, January 2008.
- V. Bruni, B. Piccoli, D. Vitulano (2008). A fast computation method for time scale signal denoising. Signal Image and Video Processing, Springer (online version), ISSN 1863-1703 (Print) 1863-1711 (Online), June 2008.
- V. Bruni, B. Piccoli, D. Vitulano (2006). Scale Space Atoms for Signals and Image De-noising. IAC Report N. 86 (2/2006)