Idea: the average B of K blocks bk aligned in K successive frames {fk}k=0,1,..,K is equivalent to the convolution of the reference block b0 (i.e. lying in the reference frame f0) with a Dirac comb kernel:

that yields:

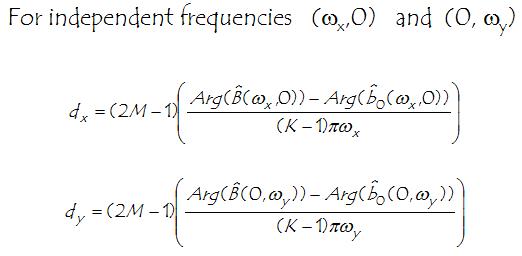
Advantages:
by V. Bruni, D. de Canditiis, and D. Vitulano
Idea: the average B of K blocks bk aligned in K successive frames {fk}k=0,1,..,K is equivalent to the convolution of the reference block b0 (i.e. lying in the reference frame f0) with a Dirac comb kernel:

that yields:

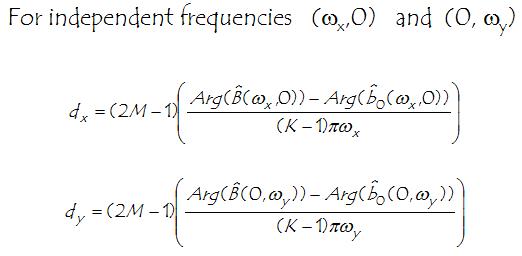
Advantages:
The equality above becomes:
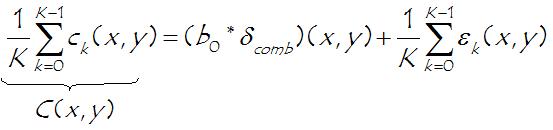
where

but
We can then associate an error to the horizontal motion component dy (and similarly an error to the vertical motion component dx). The latter is a derived measure of the noisy blocks (see references for details). It can be proven that the error can be upperbounded by the quantity:
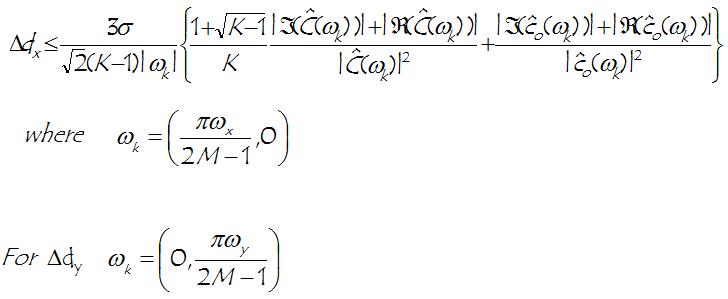


But SNR at low frequencies can be further increased using a space-filling curve.
A space-filling curve passes through each point of a 2D region producing a more correlated 1D signal!
Typical examples are:

However, each block of the image has to be modelled through a suitable curve, that accounts for the presence of a main edge inside the block.

The aim is to increase the clean signal correlation without performing denoising. Hence, we propose the two following curves

Bearing in mind the example above, we then have the two following 1D signals using respectively (from left to right) the vertical and horizontal scan:
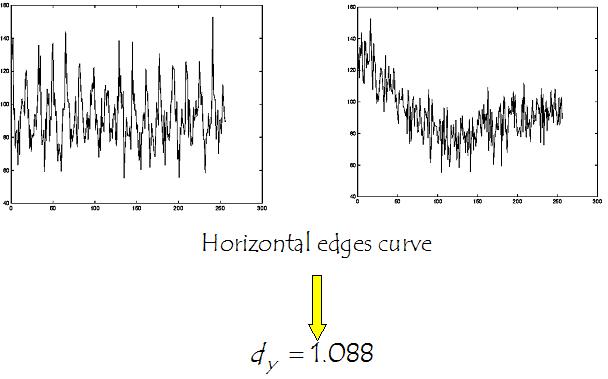

Mepi's performance on Footbal, Foreman and Flower are listed below. Mepi [1,2] has been also compared with classical Phase Correlation Algorithm (PCA)[3], Phase Difference Method (PDM) [4], 2bit (2BT) [5] and Block Matching Algorithm [6].

Look at the original and (MEPI) motion compensated sequences

Look at the original and (MEPI) motion compensated sequences
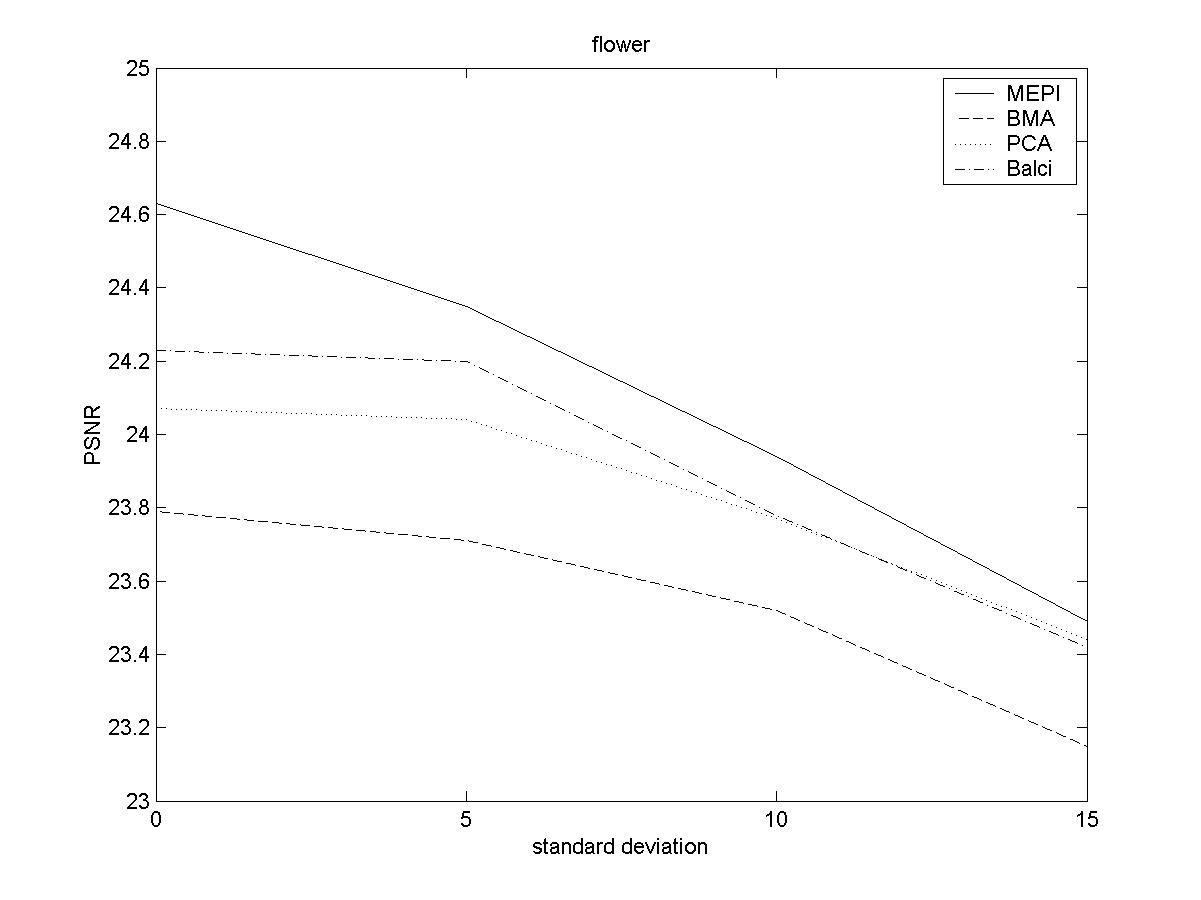
Look at the original and (MEPI) motion compensated sequences



Without noise, MEPI has a complexity lower than available motion estimation approaches:

In case of noise, the computation is still lower than alternative methods. The complexity is:
if K=2 then 8.4414 operations per pixel are required
Detailed decription about MEPI's complexity

References: